
Alternating voltage may be generated by rotating a coil in a magnetic field or by rotating a magnetic field within a stationary coil. The value of the voltage generated depends, in-each case, upon the number of turns in the coil, strength of the field and the speed at which the coil or magnetic field rotates.
Equations of the Alternating Voltages and Currents:
Consider a rectangular coil having N turns and rotating in a uniform magnetic field with an angular velocity of ω radian / second as shown in Figure. Maximum flux Φm is linked with the coil when its place coincides with the X-axis.
In time t seconds, this coil rotates through an angle θ = ωt.
In this deflected position, the component of the flux which is perpendicular to the plane of the coil is Φ = Φ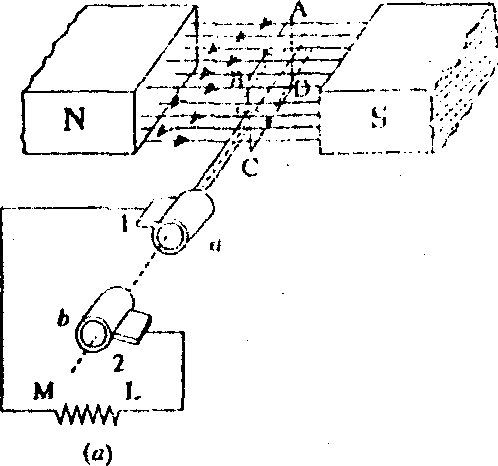 m cos ωt.
m cos ωt.
 m cos ωt.
m cos ωt.
Hence, flux linkages of the coil at any time are NΦ = NΦm cos ωt.
According to Faraday's Laws of Electromagnetic Induction, the e.m.f induced in the coil is given by the rate of change of flux-linkage of the coil. Hence, the value of the induced e.m.f at this instant (i.e where θ = ωt) or the instantaneous value of the induced e.m.f is
e = ωNΦm sin ωt volt ----------(i)
When the coil has turned through 90° i.e. when θ = 90°, then sin θ = 1, hence ‘e’ has maximum value, say Em. Therefore, from above equation we get
Em = ωNΦm = 2лfNBmA volt
f= frequency of rotation of the coil in rev/second. Substituting this value of E in Eq (i) we get
e = Em sin ωt
Similarly, the equation of the induced alternating current is
i = Im sin ωt
provided the coil circuit has been closed through a resistive load.









0 comments:
Post a Comment